|
| 1 | +#### 动态规划问题详解 |
| 2 | + |
| 3 | +##### 前言 |
| 4 | + |
| 5 | +在找工作笔试刷题的过程中,对于动态规划问题不熟悉,找了很多资料,最终发现知乎上的一个回答不错,这里对其进行简单总结。 |
| 6 | + |
| 7 | +原回答链接如下:<https://www.zhihu.com/question/23995189> |
| 8 | + |
| 9 | +##### 生活中的动态规划 |
| 10 | + |
| 11 | +先来看看生活中经常遇到的事吧——假设您是个土豪,身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w,需要用到尽量少的钞票。 |
| 12 | + |
| 13 | +依据生活经验,我们显然可以采取这样的策略:能用100的就尽量用100的,否则尽量用50的……依次类推。在这种策略下,666=6×100+1×50+1×10+1×5+1×1,共使用了10张钞票。 |
| 14 | + |
| 15 | +这种策略称为“贪心”:假设我们面对的局面是“需要凑出w”,贪心策略会尽快让w变得更小。能让w少100就尽量让它少100,这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明,贪心策略是正确的。 |
| 16 | + |
| 17 | +但是,如果我们换一组钞票的面值,贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11,那么我们在凑出15的时候,贪心策略会出错: |
| 18 | + * 15=1×11+4×1 (贪心策略使用了5张钞票) |
| 19 | + * 15=3×5 (正确的策略,只用3张钞票) |
| 20 | + |
| 21 | +为什么会这样呢?贪心策略错在了哪里? |
| 22 | + |
| 23 | +**鼠目寸光。** |
| 24 | + |
| 25 | +刚刚已经说过,贪心策略的纲领是:“尽量使接下来面对的w更小”。这样,贪心策略在w=15的局面时,会优先使用11来把w降到4;但是在这个问题中,凑出4的代价是很高的,必须使用4×1。如果使用了5,w会降为10,虽然没有4那么小,但是凑出10只需要两张5元。 |
| 26 | + |
| 27 | +在这里我们发现,贪心是一种**只考虑眼前情况**的策略。 |
| 28 | + |
| 29 | +那么,现在我们怎样才能避免鼠目寸光呢? |
| 30 | + |
| 31 | +如果直接暴力枚举凑出w的方案,明显复杂度过高。太多种方法可以凑出w了,枚举它们的时间是不可承受的。我们现在来尝试找一下性质。 |
| 32 | + |
| 33 | +重新分析刚刚的例子。w=15时,我们如果取11,接下来就面对w=4的情况;如果取5,则接下来面对w=10的情况。我们发现这些问题都有相同的形式:“给定w,凑出w所用的最少钞票是多少张?”接下来,我们用f(n)来表示“凑出n所需的最少钞票数量”。 |
| 34 | + |
| 35 | +那么,如果我们取了11,最后的代价(用掉的钞票总数)是多少呢? |
| 36 | + |
| 37 | +明显$cost=f(4)+1=4+1=5$,它的意义是:利用11来凑出15,付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。 |
| 38 | + |
| 39 | +依次类推,马上可以知道:如果我们用5来凑出15,cost就是$f(10)+1=2+1=3$ 。 |
| 40 | + |
| 41 | +那么,现在w=15的时候,我们该取那种钞票呢?**当然是各种方案中,cost值最低的那一个**! |
| 42 | + |
| 43 | + - 取11:$cost =f(4)+1=4+1=5$ |
| 44 | + - 取5:$cost =f(10)+1=2+1=3$ |
| 45 | + - 取1:$cost =f(14)+1=4+1=5$ |
| 46 | + |
| 47 | +显而易见,cost值最低的是取5的方案。**我们通过上面三个式子,做出了正确的决策**! |
| 48 | + |
| 49 | +这给了我们一个**至关重要**的启示——$f(n)$ 只与$f(n-1),f(n-5),f(n-11)$ 相关;更确切地说: |
| 50 | +$$ |
| 51 | +f(n)=min\{f(n-1),f(n-5),f(n-11)\}+1 |
| 52 | +$$ |
| 53 | + |
| 54 | +这个式子是非常激动人心的。我们要求出$f(n)$,只需要求出几个更小的f值;既然如此,我们从小到大把所有的f(i)求出来不就好了?注意一下边界情况即可。 |
| 55 | + |
| 56 | +以n=15为例,说明过程: |
| 57 | + |
| 58 | +* n=0,自然f(0) =0; |
| 59 | + |
| 60 | +* n=1,f(1)=f(0)+1=1 |
| 61 | + |
| 62 | +* n=2,f(2)=f(1)+1=2 |
| 63 | + |
| 64 | +* n=3,f(3)=f(2)+1=2+1=3 |
| 65 | + |
| 66 | +* n=4,f(4)=f(3)+1=3+1=4 |
| 67 | + |
| 68 | +* n=5,f(5)有2种情况, |
| 69 | + |
| 70 | + * f(5)=f(4)+1=4+1=5,选5张1元的; |
| 71 | + * f(5)=f(0)+1=0+1=1,选一张5元的 |
| 72 | + * 很明显,应当选择f(5)=f(0)+1=1,选一张5元的方案 |
| 73 | + |
| 74 | +* n=6,f(6)也有两种方案, |
| 75 | + |
| 76 | + * f(6)=f(5)+1=2,选一张1元和一张5元的,5元的先选 |
| 77 | + * f(6)=f(1)+1=2,选一张1元和一张5元的,1元的先选 |
| 78 | + |
| 79 | +* n=7,f(7)=f(6)+1=2+1=3(选两张1元和一张5元的),f(7)=f(2)+1=3(选2张1元的和一张5元的) |
| 80 | + |
| 81 | +* n=8,f(8)=f(7)+1=3+1=4(选三张1元和一张5元的)f(8)=f(3)+1=4(选三张1元的和一张5元的) |
| 82 | + |
| 83 | +* n=9,f(9)=f(8)+1=4+1=5(选四张1元和一张5元的),f(9)=f(4)+1=5(选4张一元的和一张5元的) |
| 84 | + |
| 85 | +* n=10,2种情况: |
| 86 | + |
| 87 | + * f(10)=f(9)+1=4+1=5(选五张1元和一张5元的) |
| 88 | + * f(10)=f(5)+1=1+1=2(选两张5元的) |
| 89 | + * * 最终,f(10)=2 |
| 90 | + |
| 91 | +* n=11,3种情况: |
| 92 | + |
| 93 | + * f(11)=f(10)+1=2+1=3(选两张5元和一张1元的) |
| 94 | + * f(11)=f(6)+1=2+1=3(选两张5元的和一张1元的) |
| 95 | + * f(11)=f(0)+1=1(选1张11元的) |
| 96 | + * 最终,f(11)=1 |
| 97 | + |
| 98 | + |
| 99 | +* n=12,3种情况: |
| 100 | + |
| 101 | + * f(12)=f(11)+1=1+1=2(选一张11元和一张1元的) |
| 102 | + * f(12)=f(7)+1=3+1=4(选两张5元的和2张1元的) |
| 103 | + * f(12)=f(11)+1=1+1=2(选一张11元和一张1元的) |
| 104 | + * 最终,f(12)=2 |
| 105 | + |
| 106 | +* n=13,3种情况: |
| 107 | + |
| 108 | + * f(13)=f(12)+1=2+1=3(选一张11元和两张1元的) |
| 109 | + * f(13)=f(8)+1=4+1=5(选两张5元的和3张1元的) |
| 110 | + * f(13)=f(3)+1=3+1=4(选一张11元和三张1元的) |
| 111 | + * 最终,f(13)=3 |
| 112 | + |
| 113 | +* n=14,3种情况: |
| 114 | + |
| 115 | + * f(14)=f(13)+1=3+1=4(选一张11元和三张1元的) |
| 116 | + * f(14)=f(9)+1=4+1=5(选两张5元的和四张1元的) |
| 117 | + * f(14)=f(3)+1=3+1=4(选一张11元和三张1元的) |
| 118 | + * 最终,f(14)=4 |
| 119 | + |
| 120 | +* n=15,3种情况: |
| 121 | + |
| 122 | + * f(15)=f(14)+1=4+1=5(选一张11元和四张1元的) |
| 123 | + * f(15)=f(10)+1=2+1=3(选三张5元的) |
| 124 | + * f(15)=f(4)+1=4+1=5(选一张11元和四张1元的) |
| 125 | + * 最终,f(15)=3 |
| 126 | + |
| 127 | +我们以$O(n)$ 的复杂度解决了这个问题。现在回过头来,我们看看它的原理: |
| 128 | + |
| 129 | + - !$f(n)$ 只与$f(n-1),f(n-5),f(n-11)$的值相关。 |
| 130 | + - 我们只关心$f(w)$ 的**值**,不关心是怎么凑出w的。 |
| 131 | + |
| 132 | + 这两个事实,保证了我们做法的正确性。它比起贪心策略,会分别算出取1、5、11的代价,从而做出一个正确决策,这样就避免掉了“鼠目寸光”! |
| 133 | + |
| 134 | + 它与暴力的区别在哪里?我们的暴力枚举了“使用的硬币”,然而这属于冗余信息。我们要的是答案,根本不关心这个答案是怎么凑出来的。譬如,要求出f(15),只需要知道f(14),f(10),f(4)的值。**其他信息并不需要。**我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n). |
| 135 | + |
| 136 | + 我们能这样干,取决于问题的性质:求出f(n),只需要知道几个更小的f(c)。**我们将求解f(c)称作求解f(n)的“子问题”。** |
| 137 | + |
| 138 | + **这就是DP**(动态规划,dynamic programming). |
| 139 | + |
| 140 | + **将一个问题拆成几个子问题,分别求解这些子问题,即可推断出大问题的解**。 |
| 141 | + |
| 142 | +> 思考题:请稍微修改代码,输出我们凑出w的**方案**。 |
| 143 | +
|
| 144 | +#### 2. 几个简单的概念 |
| 145 | + |
| 146 | +【无后效性】 |
| 147 | + |
| 148 | +一旦f(n)确定,“我们如何凑出f(n)”就再也用不着了。 |
| 149 | + |
| 150 | +要求出f(15),只需要知道f(14),f(10),f(4)的值,而f(14),f(10),f(4)是如何算出来的,对之后的问题没有影响。 |
| 151 | + |
| 152 | +**“未来与过去无关”,**这就是**无后效性**。 |
| 153 | + |
| 154 | +(严格定义:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。) |
| 155 | + |
| 156 | + |
| 157 | + |
| 158 | +【最优子结构】 |
| 159 | + |
| 160 | +回顾我们对f(n)的定义:我们记“凑出n所需的**最少**钞票数量”为f(n). |
| 161 | + |
| 162 | +f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的**最优**解,我们即可算出w=15的**最优**解。 |
| 163 | + |
| 164 | +大问题的**最优解**可以由小问题的**最优解**推出,这个性质叫做“最优子结构性质”。 |
| 165 | + |
| 166 | +引入这两个概念之后,我们如何判断一个问题能否使用DP解决呢? |
| 167 | + |
| 168 | + |
| 169 | + |
| 170 | +**能将大问题拆成几个小问题,且满足无后效性、最优子结构性质。** |
| 171 | + |
| 172 | +#### **3. DP的典型应用:DAG最短路** |
| 173 | + |
| 174 | + 问题很简单:给定一个城市的地图,所有的道路都是单行道,而且不会构成环。每条道路都有过路费,问您从S点到T点花费的最少费用。 |
| 175 | + |
| 176 | +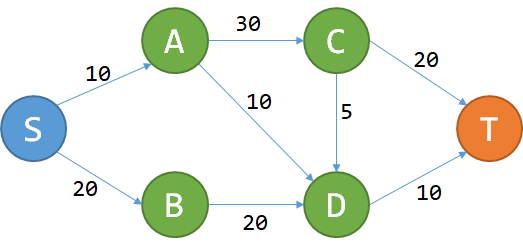 |
| 177 | + |
| 178 | + |
| 179 | + |
| 180 | +一张地图。边上的数字表示过路费。 |
| 181 | + |
| 182 | +这个问题能用DP解决吗?我们先试着记从S到P的最少费用为f(P). |
| 183 | + |
| 184 | +想要到T,要么经过C,要么经过D。从而$f(T)=min\{f(C)+20,f(D)+10\}$![. |
| 185 | + |
| 186 | +好像看起来可以DP。现在我们检验刚刚那两个性质: |
| 187 | + - 无后效性:对于点P,一旦f(P)确定,以后就只关心f(P)的值,不关心怎么去的。 |
| 188 | + - 最优子结构:对于P,我们当然只关心到P的最小费用,即f(P)。如果我们从S走到T是$S\to P\to Q \to T$ ,那肯定S走到Q的最优路径是$S \to P \to Q$ ) 。对一条最优的路径而言,从S走到**沿途上所有的点(子问题)**的最优路径,都是这条大路的一部分。这个问题的最优子结构性质是显然的。 |
| 189 | + |
| 190 | + 既然这两个性质都满足,那么本题可以DP。式子明显为: |
| 191 | +$$ |
| 192 | +f(P)=min\{f(R)+w_{R\to P}\} |
| 193 | +$$ |
| 194 | + |
| 195 | + |
| 196 | + 其中R为有路通到P的所有的点,$w_{R\to P}$ 为R到P的过路费。 |
| 197 | + |
| 198 | +手动分析过程如下: |
| 199 | + |
| 200 | +* f(S)=0 |
| 201 | + |
| 202 | +* f(A)=f(S)+10=10; |
| 203 | +* f(B)=f(S)+20=20; |
| 204 | +* f(C)=f(A)+30=10+30=40; |
| 205 | +* f(D)=min(f(A)+10,f(C)+5,f(B)+20)=min(20,45,40)=20, |
| 206 | +* f(T)=min(f(C)+20,f(D)+10)=min(60,30)=30 |
| 207 | + |
| 208 | + |
| 209 | + |
| 210 | +#### 4. 对DP原理的一点讨论 |
| 211 | + |
| 212 | +【DP的核心思想】 |
| 213 | + |
| 214 | + DP为什么会快? |
| 215 | + 无论是DP还是暴力,我们的算法都是在**可能解空间**内,寻找**最优解**。 |
| 216 | + |
| 217 | + 来看钞票问题。暴力做法是枚举所有的可能解,这是最大的可能解空间。 |
| 218 | + DP是枚举**有希望成为答案的解**。这个空间比暴力的小得多。 |
| 219 | + |
| 220 | + 也就是说:DP自带剪枝。 |
| 221 | + |
| 222 | + DP舍弃了一大堆不可能成为最优解的答案。譬如: |
| 223 | + 15 = 5+5+5 被考虑了。 |
| 224 | + 15 = 5+5+1+1+1+1+1 从来没有考虑过,因为这不可能成为最优解。 |
| 225 | + |
| 226 | + 从而我们可以得到DP的核心思想:**尽量缩小可能解空间。** |
| 227 | + |
| 228 | + 在暴力算法中,可能解空间往往是指数级的大小;如果我们采用DP,那么有可能把解空间的大小降到多项式级。 |
| 229 | + |
| 230 | + 一般来说,解空间越小,寻找解就越快。这样就完成了优化。 |
| 231 | + |
| 232 | + |
| 233 | + |
| 234 | +【DP的操作过程】 |
| 235 | + |
| 236 | + 一言以蔽之:**大事化小,小事化了。** |
| 237 | + |
| 238 | + 将一个大问题转化成几个小问题; |
| 239 | + 求解小问题; |
| 240 | + 推出大问题的解。 |
| 241 | + |
| 242 | +【如何设计DP算法】 |
| 243 | + |
| 244 | + 下面介绍比较通用的设计DP算法的步骤。 |
| 245 | + |
| 246 | + 首先,把我们面对的**局面**表示为x。这一步称为**设计状态**。 |
| 247 | + 对于状态x,记我们要求出的答案(e.g. 最小费用)为f(x).我们的目标是求出f(T). |
| 248 | +**找出f(x)与哪些局面有关(记为p)**,写出一个式子(称为**状态转移方程**),通过f(p)来推出f(x). |
| 249 | + |
| 250 | +【DP三连】 |
| 251 | + |
| 252 | + 设计DP算法,往往可以遵循DP三连: |
| 253 | + |
| 254 | + 我是谁? ——设计状态,表示局面 |
| 255 | + 我从哪里来? |
| 256 | + 我要到哪里去? ——设计转移 |
| 257 | + |
| 258 | + 设计状态是DP的基础。接下来的设计转移,有两种方式:一种是考虑我从哪里来(本文之前提到的两个例子,都是在考虑“我从哪里来”);另一种是考虑我到哪里去,这常见于求出f(x)之后,**更新能从x走到的一些解**。这种DP也是不少的,我们以后会遇到。 |
| 259 | + |
| 260 | + 总而言之,“我从哪里来”和“我要到哪里去”只需要考虑清楚其中一个,就能设计出状态转移方程,从而写代码求解问题。前者又称pull型的转移,后者又称push型的转移。(这两个词是 |
| 261 | + |
| 262 | + |
| 263 | + 妹妹告诉我的,不知道源出处在哪) |
| 264 | + |
| 265 | + |
| 266 | + |
| 267 | +> 思考题:如何把钞票问题的代码改写成“我到哪里去”的形式? |
| 268 | +> 提示:求出f(x)之后,更新f(x+1),f(x+5),f(x+11). |
| 269 | +
|
| 270 | + |
| 271 | + |
| 272 | +#### 5. 例题:最长上升子序列 |
| 273 | + |
| 274 | + 扯了这么多形而上的内容,还是做一道例题吧。 |
| 275 | + |
| 276 | + 最长上升子序列(LIS)问题:给定长度为n的序列a,从a中抽取出一个子序列,这个子序列需要单调递增。问最长的上升子序列(LIS)的长度。 |
| 277 | + e.g. 1,5,3,4,6,9,7,8的LIS为1,3,4,6,7,8,长度为6。 |
| 278 | + |
| 279 | + 如何设计状态(我是谁)? |
| 280 | + |
| 281 | + 我们记$f(x)$为以$a_x$ 结尾的LIS长度,那么答案就是$max\{f(x)\}$ |
| 282 | + |
| 283 | + 状态x从哪里推过来(我从哪里来)? |
| 284 | + |
| 285 | + 考虑比x小的每一个p:如果$a_x>a_p$ ,那么f(x)可以取f(p)+1. |
| 286 | + 解释:我们把$a_x$ 接在$a_p$ 的后面,肯定能构造一个以$a_x$ 结尾的上升子序列,长度比以$a_p$ 结尾的LIS大1.那么,我们可以写出状态转移方程了: |
| 287 | +$$ |
| 288 | +f(x)=\mathop{max}_{p<x,a_p<a_x}\{f(p)\}+1 |
| 289 | +$$ |
| 290 | + |
| 291 | + |
| 292 | + 至此解决问题。两层for循环,复杂度$O(n^2)$ |
| 293 | + |
| 294 | +手动推导过程如下: |
| 295 | + |
| 296 | +* a=1时,因为a最小,所以f(1)=1 |
| 297 | +* a=5时,f(5)=f(1)+1=2 |
| 298 | +* a=3时,因为比5小,所以只能f(3)=f(1)+1=2 |
| 299 | +* a=4时,因为比5小,比3大,所以f(4)=max(f(1)+1,f(3)+1)=max(2,3)=3 |
| 300 | +* a=6时,因为目前是最大的,所以f(6)=max(f(1)+1,f(5)+1,f(3)+1,f(4)+1)=max(2,3,3,4)=4 |
| 301 | +* a=9时,因为是目前最大的,所以f(9)=max(f(1)+1,f(5)+1,f(3)+1,f(4)+1,f(6)+1)=max(2,3,3,4,5)=5 |
| 302 | +* a=7时,因为仅比9小,所以f(7)=max(f(1)+1,f(5)+1,f(3)+1,f(4)+1,f(6)+1)=max(2,3,3,4,5)=5 |
| 303 | +* a=8时,因为仅比9小,所以f(8)=max(f(1)+1,f(5)+1,f(3)+1,f(4)+1,f(6)+1,f(7)+1)=max(2,3,3,4,5,6)=6 |
| 304 | + |
| 305 | +所以,最长上升字串元素个数是6,对应的字串是1,3,4,6,7,8 |
| 306 | + |
| 307 | +下面,针对列出的2个实例,给出java版的解决方案 |
0 commit comments