 +
+
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
+ ++
Example 1:
+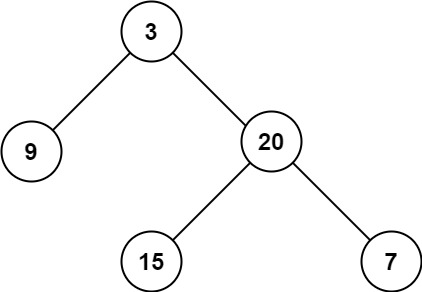 +
++Input: root = [3,9,20,null,null,15,7] +Output: 3 ++ +
Example 2:
+ ++Input: root = [1,null,2] +Output: 2 ++ +
+
Constraints:
+ +[0, 104].-100 <= Node.val <= 100
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
+
Example 1:
+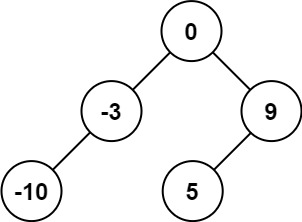 +
++Input: nums = [-10,-3,0,5,9] +Output: [0,-3,9,-10,null,5] +Explanation: [0,-10,5,null,-3,null,9] is also accepted: ++ ++
Example 2:
+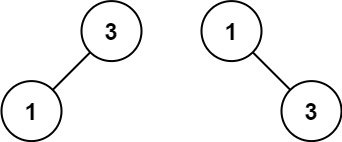 +
++Input: nums = [1,3] +Output: [3,1] +Explanation: [1,null,3] and [3,1] are both height-balanced BSTs. ++ +
+
Constraints:
+ +1 <= nums.length <= 104-104 <= nums[i] <= 104nums is sorted in a strictly increasing order.
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
+ +Return the maximum amount of water a container can store.
+ +Notice that you may not slant the container.
+ ++
Example 1:
+ +
++Input: height = [1,8,6,2,5,4,8,3,7] +Output: 49 +Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49. ++ +
Example 2:
+ ++Input: height = [1,1] +Output: 1 ++ +
+
Constraints:
+ +n == height.length2 <= n <= 1050 <= height[i] <= 104
Given a binary tree, determine if it is height-balanced.
+ ++
Example 1:
+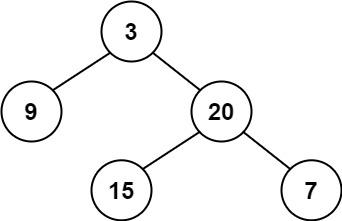 +
++Input: root = [3,9,20,null,null,15,7] +Output: true ++ +
Example 2:
+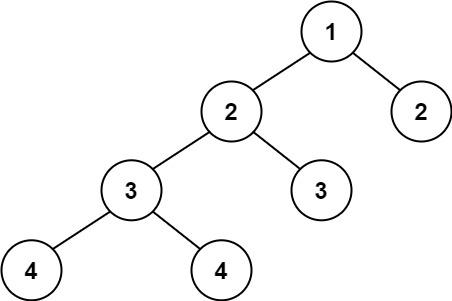 +
++Input: root = [1,2,2,3,3,null,null,4,4] +Output: false ++ +
Example 3:
+ ++Input: root = [] +Output: true ++ +
+
Constraints:
+ +[0, 5000].-104 <= Node.val <= 104
Given an integer numRows, return the first numRows of Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
+ +
++
Example 1:
+Input: numRows = 5 +Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] +
Example 2:
+Input: numRows = 1 +Output: [[1]] ++
+
Constraints:
+ +1 <= numRows <= 30
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
+ +The path sum of a path is the sum of the node's values in the path.
+ +Given the root of a binary tree, return the maximum path sum of any non-empty path.
+
Example 1:
+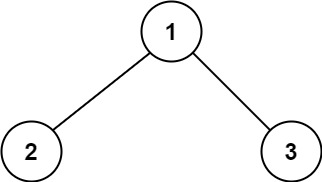 +
++Input: root = [1,2,3] +Output: 6 +Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6. ++ +
Example 2:
+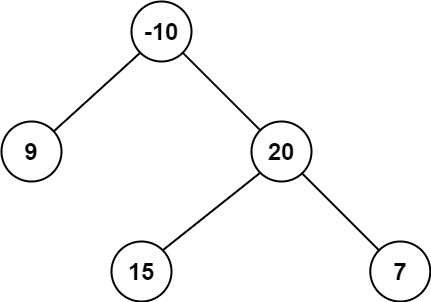 +
++Input: root = [-10,9,20,null,null,15,7] +Output: 42 +Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42. ++ +
+
Constraints:
+ +[1, 3 * 104].-1000 <= Node.val <= 1000
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
+
Example 1:
+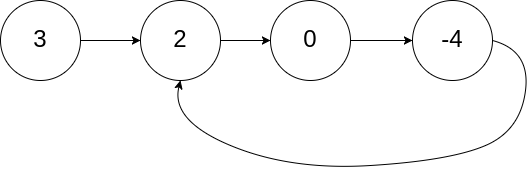 +
++Input: head = [3,2,0,-4], pos = 1 +Output: true +Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed). ++ +
Example 2:
+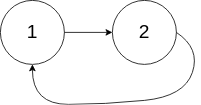 +
++Input: head = [1,2], pos = 0 +Output: true +Explanation: There is a cycle in the linked list, where the tail connects to the 0th node. ++ +
Example 3:
+ +
++Input: head = [1], pos = -1 +Output: false +Explanation: There is no cycle in the linked list. ++ +
+
Constraints:
+ +[0, 104].-105 <= Node.val <= 105pos is -1 or a valid index in the linked-list.+
Follow up: Can you solve it using O(1) (i.e. constant) memory?

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
+ ++
Example 1:
+ +
++Input: head = [3,2,0,-4], pos = 1 +Output: tail connects to node index 1 +Explanation: There is a cycle in the linked list, where tail connects to the second node. ++ +
Example 2:
+ +
++Input: head = [1,2], pos = 0 +Output: tail connects to node index 0 +Explanation: There is a cycle in the linked list, where tail connects to the first node. ++ +
Example 3:
+ +
++Input: head = [1], pos = -1 +Output: no cycle +Explanation: There is no cycle in the linked list. ++ +
+
Constraints:
+ +[0, 104].-105 <= Node.val <= 105pos is -1 or a valid index in the linked-list.+
Follow up: Can you solve it using O(1) (i.e. constant) memory?

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j's such that j != i and nums[j] < nums[i].
Return the answer in an array.
+ ++
Example 1:
+ ++Input: nums = [8,1,2,2,3] +Output: [4,0,1,1,3] +Explanation: +For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). +For nums[1]=1 does not exist any smaller number than it. +For nums[2]=2 there exist one smaller number than it (1). +For nums[3]=2 there exist one smaller number than it (1). +For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2). ++ +
Example 2:
+ ++Input: nums = [6,5,4,8] +Output: [2,1,0,3] ++ +
Example 3:
+ ++Input: nums = [7,7,7,7] +Output: [0,0,0,0] ++ +
+
Constraints:
+ +2 <= nums.length <= 5000 <= nums[i] <= 100
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
+ ++
Example 1:
+ ++Input: nums = [-1,0,1,2,-1,-4] +Output: [[-1,-1,2],[-1,0,1]] +Explanation: +nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0. +nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0. +nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0. +The distinct triplets are [-1,0,1] and [-1,-1,2]. +Notice that the order of the output and the order of the triplets does not matter. ++ +
Example 2:
+ ++Input: nums = [0,1,1] +Output: [] +Explanation: The only possible triplet does not sum up to 0. ++ +
Example 3:
+ ++Input: nums = [0,0,0] +Output: [[0,0,0]] +Explanation: The only possible triplet sums up to 0. ++ +
+
Constraints:
+ +3 <= nums.length <= 3000-105 <= nums[i] <= 105
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2] if it was rotated 4 times.[0,1,2,4,5,6,7] if it was rotated 7 times.Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array.
You must write an algorithm that runs in O(log n) time.
+
Example 1:
+ ++Input: nums = [3,4,5,1,2] +Output: 1 +Explanation: The original array was [1,2,3,4,5] rotated 3 times. ++ +
Example 2:
+ ++Input: nums = [4,5,6,7,0,1,2] +Output: 0 +Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times. ++ +
Example 3:
+ ++Input: nums = [11,13,15,17] +Output: 11 +Explanation: The original array was [11,13,15,17] and it was rotated 4 times. ++ +
+
Constraints:
+ +n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums are unique.nums is sorted and rotated between 1 and n times.
Given an integer array nums of length n and an integer target, find three integers in nums such that the sum is closest to target.
Return the sum of the three integers.
+ +You may assume that each input would have exactly one solution.
+ ++
Example 1:
+ ++Input: nums = [-1,2,1,-4], target = 1 +Output: 2 +Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2). ++ +
Example 2:
+ ++Input: nums = [0,0,0], target = 1 +Output: 0 +Explanation: The sum that is closest to the target is 0. (0 + 0 + 0 = 0). ++ +
+
Constraints:
+ +3 <= nums.length <= 500-1000 <= nums[i] <= 1000-104 <= target <= 104
Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.
For example, the following two linked lists begin to intersect at node c1:
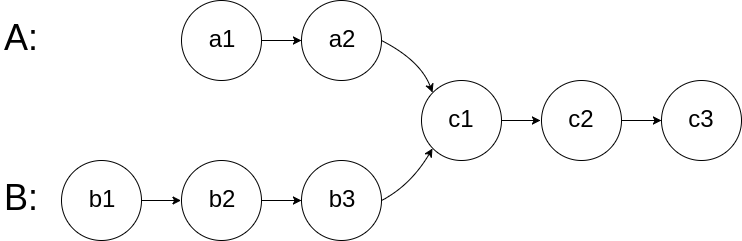 +
+The test cases are generated such that there are no cycles anywhere in the entire linked structure.
+ +Note that the linked lists must retain their original structure after the function returns.
+ +Custom Judge:
+ +The inputs to the judge are given as follows (your program is not given these inputs):
+ +intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.listA - The first linked list.listB - The second linked list.skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.
+
Example 1:
+ +
++Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 +Output: Intersected at '8' +Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). +From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B. +- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory. ++ +
Example 2:
+ +
++Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 +Output: Intersected at '2' +Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). +From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B. ++ +
Example 3:
+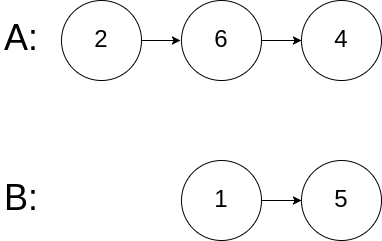 +
++Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 +Output: No intersection +Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values. +Explanation: The two lists do not intersect, so return null. ++ +
+
Constraints:
+ +listA is in the m.listB is in the n.1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= nintersectVal is 0 if listA and listB do not intersect.intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.+Follow up: Could you write a solution that runs in
O(m + n) time and use only O(1) memory?
\ No newline at end of file
diff --git a/160-intersection-of-two-linked-lists/intersection-of-two-linked-lists.cpp b/160-intersection-of-two-linked-lists/intersection-of-two-linked-lists.cpp
new file mode 100644
index 0000000000000..9f7c909ba588e
--- /dev/null
+++ b/160-intersection-of-two-linked-lists/intersection-of-two-linked-lists.cpp
@@ -0,0 +1,20 @@
+/**
+ * Definition for singly-linked list.
+ * struct ListNode {
+ * int val;
+ * ListNode *next;
+ * ListNode(int x) : val(x), next(NULL) {}
+ * };
+ */
+class Solution {
+public:
+ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
+ ListNode *p1 = headA, *p2 = headB;
+ while(p1 != p2)
+ {
+ p1 = p1 == nullptr ? headB : p1->next;
+ p2 = p2 == nullptr ? headA : p2->next;
+ }
+ return p1;
+ }
+};
diff --git a/18-4sum/4sum.cpp b/18-4sum/4sum.cpp
new file mode 100644
index 0000000000000..99e2cf753ffac
--- /dev/null
+++ b/18-4sum/4sum.cpp
@@ -0,0 +1,30 @@
+class Solution {
+public:
+ vector
Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
0 <= a, b, c, d < na, b, c, and d are distinct.nums[a] + nums[b] + nums[c] + nums[d] == targetYou may return the answer in any order.
+ ++
Example 1:
+ ++Input: nums = [1,0,-1,0,-2,2], target = 0 +Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]] ++ +
Example 2:
+ ++Input: nums = [2,2,2,2,2], target = 8 +Output: [[2,2,2,2]] ++ +
+
Constraints:
+ +1 <= nums.length <= 200-109 <= nums[i] <= 109-109 <= target <= 109
Given the head of a singly linked list, reverse the list, and return the reversed list.
+
Example 1:
+ +
++Input: head = [1,2,3,4,5] +Output: [5,4,3,2,1] ++ +
Example 2:
+ +
++Input: head = [1,2] +Output: [2,1] ++ +
Example 3:
+ ++Input: head = [] +Output: [] ++ +
+
Constraints:
+ +[0, 5000].-5000 <= Node.val <= 5000+
Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?
diff --git a/206-reverse-linked-list/reverse-linked-list.cpp b/206-reverse-linked-list/reverse-linked-list.cpp new file mode 100644 index 0000000000000..4fad719bf7805 --- /dev/null +++ b/206-reverse-linked-list/reverse-linked-list.cpp @@ -0,0 +1,24 @@ +/** + * Definition for singly-linked list. + * struct ListNode { + * int val; + * ListNode *next; + * ListNode() : val(0), next(nullptr) {} + * ListNode(int x) : val(x), next(nullptr) {} + * ListNode(int x, ListNode *next) : val(x), next(next) {} + * }; + */ +class Solution { +public: + ListNode* reverseList(ListNode* head) { + ListNode* curr=head; + ListNode* prev=NULL; + while(curr){ + ListNode* temp=curr->next; + curr->next=prev; + prev=curr; + curr=temp; + } + return prev; + } +}; \ No newline at end of file diff --git a/2144-maximum-difference-between-increasing-elements/README.md b/2144-maximum-difference-between-increasing-elements/README.md new file mode 100644 index 0000000000000..783f8740f7073 --- /dev/null +++ b/2144-maximum-difference-between-increasing-elements/README.md @@ -0,0 +1,41 @@ +
Given a 0-indexed integer array nums of size n, find the maximum difference between nums[i] and nums[j] (i.e., nums[j] - nums[i]), such that 0 <= i < j < n and nums[i] < nums[j].
Return the maximum difference. If no such i and j exists, return -1.
+
Example 1:
+ ++Input: nums = [7,1,5,4] +Output: 4 +Explanation: +The maximum difference occurs with i = 1 and j = 2, nums[j] - nums[i] = 5 - 1 = 4. +Note that with i = 1 and j = 0, the difference nums[j] - nums[i] = 7 - 1 = 6, but i > j, so it is not valid. ++ +
Example 2:
+ ++Input: nums = [9,4,3,2] +Output: -1 +Explanation: +There is no i and j such that i < j and nums[i] < nums[j]. ++ +
Example 3:
+ ++Input: nums = [1,5,2,10] +Output: 9 +Explanation: +The maximum difference occurs with i = 0 and j = 3, nums[j] - nums[i] = 10 - 1 = 9. ++ +
+
Constraints:
+ +n == nums.length2 <= n <= 10001 <= nums[i] <= 109
Given an integer array nums, find the maximum possible bitwise OR of a subset of nums and return the number of different non-empty subsets with the maximum bitwise OR.
An array a is a subset of an array b if a can be obtained from b by deleting some (possibly zero) elements of b. Two subsets are considered different if the indices of the elements chosen are different.
The bitwise OR of an array a is equal to a[0] OR a[1] OR ... OR a[a.length - 1] (0-indexed).
+
Example 1:
+ ++Input: nums = [3,1] +Output: 2 +Explanation: The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3: +- [3] +- [3,1] ++ +
Example 2:
+ ++Input: nums = [2,2,2] +Output: 7 +Explanation: All non-empty subsets of [2,2,2] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets. ++ +
Example 3:
+ ++Input: nums = [3,2,1,5] +Output: 6 +Explanation: The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7: +- [3,5] +- [3,1,5] +- [3,2,5] +- [3,2,1,5] +- [2,5] +- [2,1,5]+ +
+
Constraints:
+ +1 <= nums.length <= 161 <= nums[i] <= 105
A string s can be partitioned into groups of size k using the following procedure:
k characters of the string, the second group consists of the next k characters of the string, and so on. Each element can be a part of exactly one group.k characters remaining, a character fill is used to complete the group.Note that the partition is done so that after removing the fill character from the last group (if it exists) and concatenating all the groups in order, the resultant string should be s.
Given the string s, the size of each group k and the character fill, return a string array denoting the composition of every group s has been divided into, using the above procedure.
+
Example 1:
+ ++Input: s = "abcdefghi", k = 3, fill = "x" +Output: ["abc","def","ghi"] +Explanation: +The first 3 characters "abc" form the first group. +The next 3 characters "def" form the second group. +The last 3 characters "ghi" form the third group. +Since all groups can be completely filled by characters from the string, we do not need to use fill. +Thus, the groups formed are "abc", "def", and "ghi". ++ +
Example 2:
+ ++Input: s = "abcdefghij", k = 3, fill = "x" +Output: ["abc","def","ghi","jxx"] +Explanation: +Similar to the previous example, we are forming the first three groups "abc", "def", and "ghi". +For the last group, we can only use the character 'j' from the string. To complete this group, we add 'x' twice. +Thus, the 4 groups formed are "abc", "def", "ghi", and "jxx". ++ +
+
Constraints:
+ +1 <= s.length <= 100s consists of lowercase English letters only.1 <= k <= 100fill is a lowercase English letter.
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
+
Example 1:
+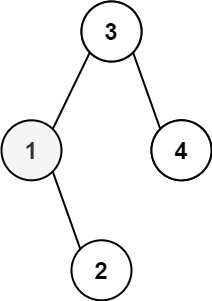 +
++Input: root = [3,1,4,null,2], k = 1 +Output: 1 ++ +
Example 2:
+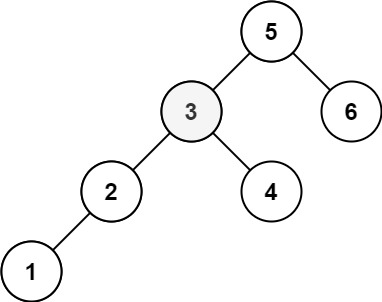 +
++Input: root = [5,3,6,2,4,null,null,1], k = 3 +Output: 3 ++ +
+
Constraints:
+ +n.1 <= k <= n <= 1040 <= Node.val <= 104+
Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
diff --git a/230-kth-smallest-element-in-a-bst/kth-smallest-element-in-a-bst.cpp b/230-kth-smallest-element-in-a-bst/kth-smallest-element-in-a-bst.cpp new file mode 100644 index 0000000000000..26854a06ee854 --- /dev/null +++ b/230-kth-smallest-element-in-a-bst/kth-smallest-element-in-a-bst.cpp @@ -0,0 +1,31 @@ +/** + * Definition for a binary tree node. + * struct TreeNode { + * int val; + * TreeNode *left; + * TreeNode *right; + * TreeNode() : val(0), left(nullptr), right(nullptr) {} + * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} + * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} + * }; + */ +class Solution { +public: + int count=0; + int res=0; + void inorder(TreeNode* root, int k){ + if(!root) return; + inorder(root->left,k); + count++; + if(count==k){ + res=root->val; + return; + } + inorder(root->right,k); + } + + int kthSmallest(TreeNode* root, int k) { + inorder(root,k); + return res; + } +}; \ No newline at end of file diff --git a/2316-count-hills-and-valleys-in-an-array/README.md b/2316-count-hills-and-valleys-in-an-array/README.md new file mode 100644 index 0000000000000..37f26609bda18 --- /dev/null +++ b/2316-count-hills-and-valleys-in-an-array/README.md @@ -0,0 +1,44 @@ +
You are given a 0-indexed integer array nums. An index i is part of a hill in nums if the closest non-equal neighbors of i are smaller than nums[i]. Similarly, an index i is part of a valley in nums if the closest non-equal neighbors of i are larger than nums[i]. Adjacent indices i and j are part of the same hill or valley if nums[i] == nums[j].
Note that for an index to be part of a hill or valley, it must have a non-equal neighbor on both the left and right of the index.
+ +Return the number of hills and valleys in nums.
+
Example 1:
+ ++Input: nums = [2,4,1,1,6,5] +Output: 3 +Explanation: +At index 0: There is no non-equal neighbor of 2 on the left, so index 0 is neither a hill nor a valley. +At index 1: The closest non-equal neighbors of 4 are 2 and 1. Since 4 > 2 and 4 > 1, index 1 is a hill. +At index 2: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 2 is a valley. +At index 3: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 3 is a valley, but note that it is part of the same valley as index 2. +At index 4: The closest non-equal neighbors of 6 are 1 and 5. Since 6 > 1 and 6 > 5, index 4 is a hill. +At index 5: There is no non-equal neighbor of 5 on the right, so index 5 is neither a hill nor a valley. +There are 3 hills and valleys so we return 3. ++ +
Example 2:
+ ++Input: nums = [6,6,5,5,4,1] +Output: 0 +Explanation: +At index 0: There is no non-equal neighbor of 6 on the left, so index 0 is neither a hill nor a valley. +At index 1: There is no non-equal neighbor of 6 on the left, so index 1 is neither a hill nor a valley. +At index 2: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 2 is neither a hill nor a valley. +At index 3: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 3 is neither a hill nor a valley. +At index 4: The closest non-equal neighbors of 4 are 5 and 1. Since 4 < 5 and 4 > 1, index 4 is neither a hill nor a valley. +At index 5: There is no non-equal neighbor of 1 on the right, so index 5 is neither a hill nor a valley. +There are 0 hills and valleys so we return 0. ++ +
+
Constraints:
+ +3 <= nums.length <= 1001 <= nums[i] <= 100
The bitwise AND of an array nums is the bitwise AND of all integers in nums.
nums = [1, 5, 3], the bitwise AND is equal to 1 & 5 & 3 = 1.nums = [7], the bitwise AND is 7.You are given an array of positive integers candidates. Compute the bitwise AND for all possible combinations of elements in the candidates array.
Return the size of the largest combination of candidates with a bitwise AND greater than 0.
+
Example 1:
+ ++Input: candidates = [16,17,71,62,12,24,14] +Output: 4 +Explanation: The combination [16,17,62,24] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0. +The size of the combination is 4. +It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0. +Note that more than one combination may have the largest size. +For example, the combination [62,12,24,14] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0. ++ +
Example 2:
+ ++Input: candidates = [8,8] +Output: 2 +Explanation: The largest combination [8,8] has a bitwise AND of 8 & 8 = 8 > 0. +The size of the combination is 2, so we return 2. ++ +
+
Constraints:
+ +1 <= candidates.length <= 1051 <= candidates[i] <= 107
There is a singly-linked list head and we want to delete a node node in it.
You are given the node to be deleted node. You will not be given access to the first node of head.
All the values of the linked list are unique, and it is guaranteed that the given node node is not the last node in the linked list.
Delete the given node. Note that by deleting the node, we do not mean removing it from memory. We mean:
+ +node should be in the same order.node should be in the same order.Custom testing:
+ +head and the node to be given node. node should not be the last node of the list and should be an actual node in the list.+
Example 1:
+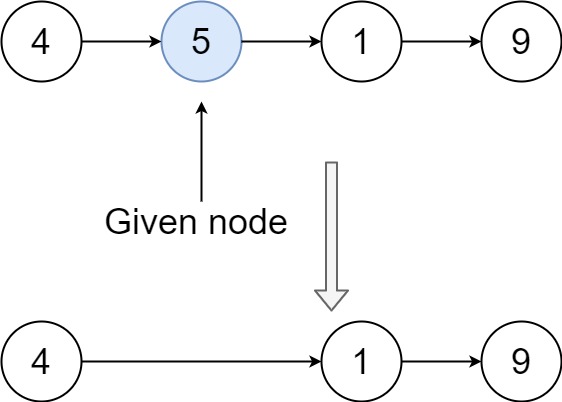 +
++Input: head = [4,5,1,9], node = 5 +Output: [4,1,9] +Explanation: You are given the second node with value 5, the linked list should become 4 -> 1 -> 9 after calling your function. ++ +
Example 2:
+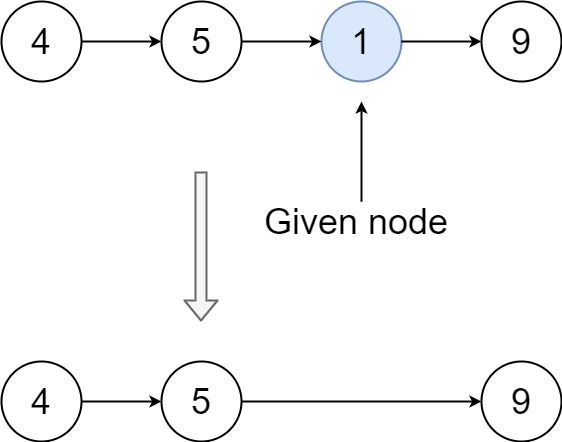 +
++Input: head = [4,5,1,9], node = 1 +Output: [4,5,9] +Explanation: You are given the third node with value 1, the linked list should become 4 -> 5 -> 9 after calling your function. ++ +
+
Constraints:
+ +[2, 1000].-1000 <= Node.val <= 1000node to be deleted is in the list and is not a tail node.
You are given an integer array nums and an integer k. You may partition nums into one or more subsequences such that each element in nums appears in exactly one of the subsequences.
Return the minimum number of subsequences needed such that the difference between the maximum and minimum values in each subsequence is at most k.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
+ ++
Example 1:
+ ++Input: nums = [3,6,1,2,5], k = 2 +Output: 2 +Explanation: +We can partition nums into the two subsequences [3,1,2] and [6,5]. +The difference between the maximum and minimum value in the first subsequence is 3 - 1 = 2. +The difference between the maximum and minimum value in the second subsequence is 6 - 5 = 1. +Since two subsequences were created, we return 2. It can be shown that 2 is the minimum number of subsequences needed. ++ +
Example 2:
+ ++Input: nums = [1,2,3], k = 1 +Output: 2 +Explanation: +We can partition nums into the two subsequences [1,2] and [3]. +The difference between the maximum and minimum value in the first subsequence is 2 - 1 = 1. +The difference between the maximum and minimum value in the second subsequence is 3 - 3 = 0. +Since two subsequences were created, we return 2. Note that another optimal solution is to partition nums into the two subsequences [1] and [2,3]. ++ +
Example 3:
+ ++Input: nums = [2,2,4,5], k = 0 +Output: 3 +Explanation: +We can partition nums into the three subsequences [2,2], [4], and [5]. +The difference between the maximum and minimum value in the first subsequences is 2 - 2 = 0. +The difference between the maximum and minimum value in the second subsequences is 4 - 4 = 0. +The difference between the maximum and minimum value in the third subsequences is 5 - 5 = 0. +Since three subsequences were created, we return 3. It can be shown that 3 is the minimum number of subsequences needed. ++ +
+
Constraints:
+ +1 <= nums.length <= 1050 <= nums[i] <= 1050 <= k <= 105
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
Return the max sliding window.
+ ++
Example 1:
+ ++Input: nums = [1,3,-1,-3,5,3,6,7], k = 3 +Output: [3,3,5,5,6,7] +Explanation: +Window position Max +--------------- ----- +[1 3 -1] -3 5 3 6 7 3 + 1 [3 -1 -3] 5 3 6 7 3 + 1 3 [-1 -3 5] 3 6 7 5 + 1 3 -1 [-3 5 3] 6 7 5 + 1 3 -1 -3 [5 3 6] 7 6 + 1 3 -1 -3 5 [3 6 7] 7 ++ +
Example 2:
+ ++Input: nums = [1], k = 1 +Output: [1] ++ +
+
Constraints:
+ +1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
You are given a string s and a robot that currently holds an empty string t. Apply one of the following operations until s and t are both empty:
s and give it to the robot. The robot will append this character to the string t.t and give it to the robot. The robot will write this character on paper.Return the lexicographically smallest string that can be written on the paper.
+ ++
Example 1:
+ ++Input: s = "zza" +Output: "azz" +Explanation: Let p denote the written string. +Initially p="", s="zza", t="". +Perform first operation three times p="", s="", t="zza". +Perform second operation three times p="azz", s="", t="". ++ +
Example 2:
+ ++Input: s = "bac" +Output: "abc" +Explanation: Let p denote the written string. +Perform first operation twice p="", s="c", t="ba". +Perform second operation twice p="ab", s="c", t="". +Perform first operation p="ab", s="", t="c". +Perform second operation p="abc", s="", t="". ++ +
Example 3:
+ ++Input: s = "bdda" +Output: "addb" +Explanation: Let p denote the written string. +Initially p="", s="bdda", t="". +Perform first operation four times p="", s="", t="bdda". +Perform second operation four times p="addb", s="", t="". ++ +
+
Constraints:
+ +1 <= s.length <= 105s consists of only English lowercase letters.
A permutation of an array of integers is an arrangement of its members into a sequence or linear order.
+ +arr = [1,2,3], the following are all the permutations of arr: [1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1].The next permutation of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the next permutation of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
+ +arr = [1,2,3] is [1,3,2].arr = [2,3,1] is [3,1,2].arr = [3,2,1] is [1,2,3] because [3,2,1] does not have a lexicographical larger rearrangement.Given an array of integers nums, find the next permutation of nums.
The replacement must be in place and use only constant extra memory.
+ ++
Example 1:
+ ++Input: nums = [1,2,3] +Output: [1,3,2] ++ +
Example 2:
+ ++Input: nums = [3,2,1] +Output: [1,2,3] ++ +
Example 3:
+ ++Input: nums = [1,1,5] +Output: [1,5,1] ++ +
+
Constraints:
+ +1 <= nums.length <= 1000 <= nums[i] <= 100
You are given an integer array nums of size n where n is a multiple of 3 and a positive integer k.
Divide the array nums into n / 3 arrays of size 3 satisfying the following condition:
k.Return a 2D array containing the arrays. If it is impossible to satisfy the conditions, return an empty array. And if there are multiple answers, return any of them.
+ ++
Example 1:
+ +Input: nums = [1,3,4,8,7,9,3,5,1], k = 2
+ +Output: [[1,1,3],[3,4,5],[7,8,9]]
+ +Explanation:
+ +The difference between any two elements in each array is less than or equal to 2.
+Example 2:
+ +Input: nums = [2,4,2,2,5,2], k = 2
+ +Output: []
+ +Explanation:
+ +Different ways to divide nums into 2 arrays of size 3 are:
Because there are four 2s there will be an array with the elements 2 and 5 no matter how we divide it. since 5 - 2 = 3 > k, the condition is not satisfied and so there is no valid division.
Example 3:
+ +Input: nums = [4,2,9,8,2,12,7,12,10,5,8,5,5,7,9,2,5,11], k = 14
+ +Output: [[2,2,12],[4,8,5],[5,9,7],[7,8,5],[5,9,10],[11,12,2]]
+ +Explanation:
+ +The difference between any two elements in each array is less than or equal to 14.
++
Constraints:
+ +n == nums.length1 <= n <= 105n is a multiple of 31 <= nums[i] <= 1051 <= k <= 105
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
+
Example 1:
+Input: nums = [4,5,6,7,0,1,2], target = 0 +Output: 4 +
Example 2:
+Input: nums = [4,5,6,7,0,1,2], target = 3 +Output: -1 +
Example 3:
+Input: nums = [1], target = 0 +Output: -1 ++
+
Constraints:
+ +1 <= nums.length <= 5000-104 <= nums[i] <= 104nums are unique.nums is an ascending array that is possibly rotated.-104 <= target <= 104
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
+
Example 1:
+Input: nums = [5,7,7,8,8,10], target = 8 +Output: [3,4] +
Example 2:
+Input: nums = [5,7,7,8,8,10], target = 6 +Output: [-1,-1] +
Example 3:
+Input: nums = [], target = 0 +Output: [-1,-1] ++
+
Constraints:
+ +0 <= nums.length <= 105-109 <= nums[i] <= 109nums is a non-decreasing array.-109 <= target <= 109
You are given a string s. It may contain any number of '*' characters. Your task is to remove all '*' characters.
While there is a '*', do the following operation:
'*' and the smallest non-'*' character to its left. If there are several smallest characters, you can delete any of them.Return the lexicographically smallest resulting string after removing all '*' characters.
+
Example 1:
+ +Input: s = "aaba*"
+ +Output: "aab"
+ +Explanation:
+ +We should delete one of the 'a' characters with '*'. If we choose s[3], s becomes the lexicographically smallest.
Example 2:
+ +Input: s = "abc"
+ +Output: "abc"
+ +Explanation:
+ +There is no '*' in the string.
+
Constraints:
+ +1 <= s.length <= 105s consists only of lowercase English letters and '*'.'*' characters.
You are given an integer array nums. You need to ensure that the elements in the array are distinct. To achieve this, you can perform the following operation any number of times:
Note that an empty array is considered to have distinct elements. Return the minimum number of operations needed to make the elements in the array distinct.
+ ++
Example 1:
+ +Input: nums = [1,2,3,4,2,3,3,5,7]
+ +Output: 2
+ +Explanation:
+ +[4, 2, 3, 3, 5, 7].[3, 5, 7], which has distinct elements.Therefore, the answer is 2.
+Example 2:
+ +Input: nums = [4,5,6,4,4]
+ +Output: 2
+ +Explanation:
+ +[4, 4].Therefore, the answer is 2.
+Example 3:
+ +Input: nums = [6,7,8,9]
+ +Output: 0
+ +Explanation:
+ +The array already contains distinct elements. Therefore, the answer is 0.
++
Constraints:
+ +1 <= nums.length <= 1001 <= nums[i] <= 100
Given a circular array nums, find the maximum absolute difference between adjacent elements.
Note: In a circular array, the first and last elements are adjacent.
+ ++
Example 1:
+ +Input: nums = [1,2,4]
+ +Output: 3
+ +Explanation:
+ +Because nums is circular, nums[0] and nums[2] are adjacent. They have the maximum absolute difference of |4 - 1| = 3.
Example 2:
+ +Input: nums = [-5,-10,-5]
+ +Output: 5
+ +Explanation:
+ +The adjacent elements nums[0] and nums[1] have the maximum absolute difference of |-5 - (-10)| = 5.
+
Constraints:
+ +2 <= nums.length <= 100-100 <= nums[i] <= 100
You are given a string s consisting of lowercase English letters.
Your task is to find the maximum difference diff = freq(a1) - freq(a2) between the frequency of characters a1 and a2 in the string such that:
a1 has an odd frequency in the string.a2 has an even frequency in the string.Return this maximum difference.
+ ++
Example 1:
+ +Input: s = "aaaaabbc"
+ +Output: 3
+ +Explanation:
+ +'a' has an odd frequency of 5, and 'b' has an even frequency of 2.5 - 2 = 3.Example 2:
+ +Input: s = "abcabcab"
+ +Output: 1
+ +Explanation:
+ +'a' has an odd frequency of 3, and 'c' has an even frequency of 2.3 - 2 = 1.+
Constraints:
+ +3 <= s.length <= 100s consists only of lowercase English letters.s contains at least one character with an odd frequency and one with an even frequency.
You are given a string s consisting of the characters 'N', 'S', 'E', and 'W', where s[i] indicates movements in an infinite grid:
'N' : Move north by 1 unit.'S' : Move south by 1 unit.'E' : Move east by 1 unit.'W' : Move west by 1 unit.Initially, you are at the origin (0, 0). You can change at most k characters to any of the four directions.
Find the maximum Manhattan distance from the origin that can be achieved at any time while performing the movements in order.
+The Manhattan Distance between two cells(xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.
++
Example 1:
+ +Input: s = "NWSE", k = 1
+ +Output: 3
+ +Explanation:
+ +Change s[2] from 'S' to 'N'. The string s becomes "NWNE".
| Movement | +Position (x, y) | +Manhattan Distance | +Maximum | +
|---|---|---|---|
| s[0] == 'N' | +(0, 1) | +0 + 1 = 1 | +1 | +
| s[1] == 'W' | +(-1, 1) | +1 + 1 = 2 | +2 | +
| s[2] == 'N' | +(-1, 2) | +1 + 2 = 3 | +3 | +
| s[3] == 'E' | +(0, 2) | +0 + 2 = 2 | +3 | +
The maximum Manhattan distance from the origin that can be achieved is 3. Hence, 3 is the output.
+Example 2:
+ +Input: s = "NSWWEW", k = 3
+ +Output: 6
+ +Explanation:
+ +Change s[1] from 'S' to 'N', and s[4] from 'E' to 'W'. The string s becomes "NNWWWW".
The maximum Manhattan distance from the origin that can be achieved is 6. Hence, 6 is the output.
++
Constraints:
+ +1 <= s.length <= 1050 <= k <= s.lengths consists of only 'N', 'S', 'E', and 'W'.
You are given two arrays of integers, fruits and baskets, each of length n, where fruits[i] represents the quantity of the ith type of fruit, and baskets[j] represents the capacity of the jth basket.
From left to right, place the fruits according to these rules:
+ +Return the number of fruit types that remain unplaced after all possible allocations are made.
+ ++
Example 1:
+ +Input: fruits = [4,2,5], baskets = [3,5,4]
+ +Output: 1
+ +Explanation:
+ +fruits[0] = 4 is placed in baskets[1] = 5.fruits[1] = 2 is placed in baskets[0] = 3.fruits[2] = 5 cannot be placed in baskets[2] = 4.Since one fruit type remains unplaced, we return 1.
+Example 2:
+ +Input: fruits = [3,6,1], baskets = [6,4,7]
+ +Output: 0
+ +Explanation:
+ +fruits[0] = 3 is placed in baskets[0] = 6.fruits[1] = 6 cannot be placed in baskets[1] = 4 (insufficient capacity) but can be placed in the next available basket, baskets[2] = 7.fruits[2] = 1 is placed in baskets[1] = 4.Since all fruits are successfully placed, we return 0.
++
Constraints:
+ +n == fruits.length == baskets.length1 <= n <= 1001 <= fruits[i], baskets[i] <= 1000
Given an integer n, return all the numbers in the range [1, n] sorted in lexicographical order.
You must write an algorithm that runs in O(n) time and uses O(1) extra space.
+
Example 1:
+Input: n = 13 +Output: [1,10,11,12,13,2,3,4,5,6,7,8,9] +
Example 2:
+Input: n = 2 +Output: [1,2] ++
+
Constraints:
+ +1 <= n <= 5 * 104
Given an integer array nums of length n where all the integers of nums are in the range [1, n] and each integer appears at most twice, return an array of all the integers that appears twice.
You must write an algorithm that runs in O(n) time and uses only constant auxiliary space, excluding the space needed to store the output
+
Example 1:
+Input: nums = [4,3,2,7,8,2,3,1] +Output: [2,3] +
Example 2:
+Input: nums = [1,1,2] +Output: [1] +
Example 3:
+Input: nums = [1] +Output: [] ++
+
Constraints:
+ +n == nums.length1 <= n <= 1051 <= nums[i] <= nnums appears once or twice.
Given an array nums of n integers where nums[i] is in the range [1, n], return an array of all the integers in the range [1, n] that do not appear in nums.
+
Example 1:
+Input: nums = [4,3,2,7,8,2,3,1] +Output: [5,6] +
Example 2:
+Input: nums = [1,1] +Output: [2] ++
+
Constraints:
+ +n == nums.length1 <= n <= 1051 <= nums[i] <= n+
Follow up: Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's.
You must do it in place.
+ ++
Example 1:
+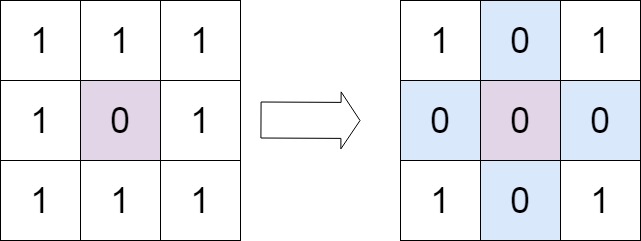 +
++Input: matrix = [[1,1,1],[1,0,1],[1,1,1]] +Output: [[1,0,1],[0,0,0],[1,0,1]] ++ +
Example 2:
+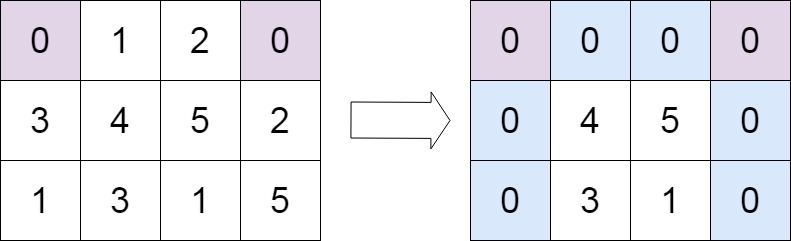 +
++Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] +Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]] ++ +
+
Constraints:
+ +m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1+
Follow up:
+ +O(mn) space is probably a bad idea.O(m + n) space, but still not the best solution.
Given an array nums with n objects colored red, white, or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
We will use the integers 0, 1, and 2 to represent the color red, white, and blue, respectively.
You must solve this problem without using the library's sort function.
+ ++
Example 1:
+ ++Input: nums = [2,0,2,1,1,0] +Output: [0,0,1,1,2,2] ++ +
Example 2:
+ ++Input: nums = [2,0,1] +Output: [0,1,2] ++ +
+
Constraints:
+ +n == nums.length1 <= n <= 300nums[i] is either 0, 1, or 2.+
Follow up: Could you come up with a one-pass algorithm using only constant extra space?
diff --git a/75-sort-colors/sort-colors.cpp b/75-sort-colors/sort-colors.cpp new file mode 100644 index 0000000000000..872c342d3cb60 --- /dev/null +++ b/75-sort-colors/sort-colors.cpp @@ -0,0 +1,20 @@ +class Solution { +public: + void sortColors(vector
Given the head of a singly linked list, return the middle node of the linked list.
If there are two middle nodes, return the second middle node.
+ ++
Example 1:
+ +
++Input: head = [1,2,3,4,5] +Output: [3,4,5] +Explanation: The middle node of the list is node 3. ++ +
Example 2:
+ +
++Input: head = [1,2,3,4,5,6] +Output: [4,5,6] +Explanation: Since the list has two middle nodes with values 3 and 4, we return the second one. ++ +
+
Constraints:
+ +[1, 100].1 <= Node.val <= 100
Given the root of a binary tree, return the inorder traversal of its nodes' values.
+
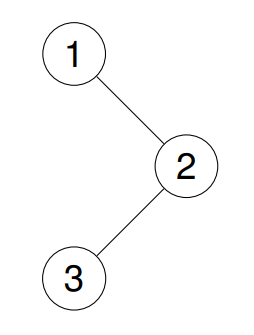
Example 1:
+ +Input: root = [1,null,2,3]
+ +Output: [1,3,2]
+ +Explanation:
+ +
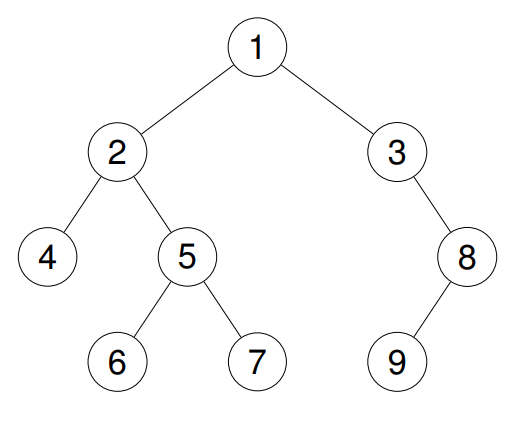
Example 2:
+ +Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
+ +Output: [4,2,6,5,7,1,3,9,8]
+ +Explanation:
+ +
Example 3:
+ +Input: root = []
+ +Output: []
+Example 4:
+ +Input: root = [1]
+ +Output: [1]
++
Constraints:
+ +[0, 100].-100 <= Node.val <= 100+Follow up: Recursive solution is trivial, could you do it iteratively? \ No newline at end of file diff --git a/94-binary-tree-inorder-traversal/binary-tree-inorder-traversal.cpp b/94-binary-tree-inorder-traversal/binary-tree-inorder-traversal.cpp new file mode 100644 index 0000000000000..358258da60415 --- /dev/null +++ b/94-binary-tree-inorder-traversal/binary-tree-inorder-traversal.cpp @@ -0,0 +1,22 @@ +/** + * Definition for a binary tree node. + * struct TreeNode { + * int val; + * TreeNode *left; + * TreeNode *right; + * TreeNode() : val(0), left(nullptr), right(nullptr) {} + * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} + * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} + * }; + */ +class Solution { +public: + vector