You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Copy file name to clipboardExpand all lines: Bubble Sort/README.markdown
+12-12Lines changed: 12 additions & 12 deletions
Display the source diff
Display the rich diff
Original file line number
Diff line number
Diff line change
@@ -11,20 +11,20 @@ Bubble sort is a sorting algorithm that is implemented by starting in the beginn
11
11
12
12
### Implementation:
13
13
14
-
The implementation will not be shown as the average and worst runtimes show that this is a very inefficient algorithm. However, having a grasp of the concept will help you understand the basics of simple sorting algorithms.
14
+
The implementation will not be shown as the average and worst runtimes indicate that this is a very inefficient algorithm. However, grasping the concept will help you understand the basics of simple sorting algorithms.
15
15
16
-
Bubble sort is a very simple sorting algorithm, it consists in comparing pairs of adjacent elements in the array, if the first element is larger, swap them, otherwise, you do nothing and go for the next comparison.
16
+
Bubble sort is a very simple sorting algorithm, only comparing pairs of adjacent elements in the array. If the first element is larger, it is swapped; otherwise, nothing occurs and you move onto the next comparison.
17
17
This is accomplished by looking through the array `n` times, `n` being the amount of elements in the array.
18
18
19
19
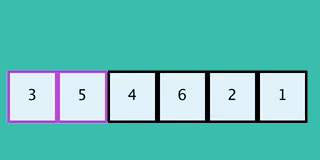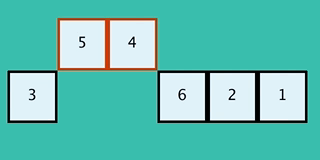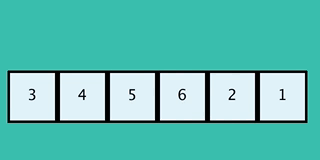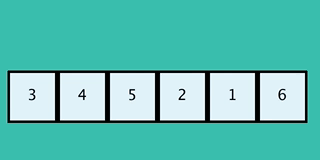
20
20
21
-
This GIF shows a inverted implementation than
21
+
This GIF shows an inverted implementation
22
22
23
23
#### Example
24
-
Let us take the array `[5, 1, 4, 2, 8]`, and sort the array from lowest number to greatest number using bubble sort. In each step, elements written in bold are being compared. Three passes will be required.
24
+
Let us take the array `[5, 1, 4, 2, 8]`, and sort the array from lowest to highest using bubble sort. For each step, the elements written in bold are being compared. In this example, three passes will be required.
25
25
26
26
##### First Pass
27
-
[**5 1** 4 2 8 ] -> [**1 5** 4 2 8 ], Here, algorithm compares the first two elements, and swaps since 5 > 1.
27
+
[**5 1** 4 2 8 ] -> [**1 5** 4 2 8 ], Here, algorithm compares the first two elements and swaps them since 5 > 1.
@@ -40,7 +40,7 @@ Let us take the array `[5, 1, 4, 2, 8]`, and sort the array from lowest number t
40
40
[ 1 2 **4 5** 8 ] -> [ 1 2 **4 5** 8 ]
41
41
42
42
[ 1 2 4 **5 8**] -> [ 1 2 4 **5 8**]
43
-
Now, the array is already sorted, but the algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
43
+
Now, the array is already sorted, but the algorithm does not know if it is completed. The algorithm needs to have one more pass without any swaps to know it is sorted.
44
44
45
45
##### Third Pass
46
46
[**1 2** 4 5 8 ] -> [**1 2** 4 5 8 ]
@@ -50,8 +50,8 @@ Now, the array is already sorted, but the algorithm does not know if it is compl
50
50
[ 1 2 **4 5** 8 ] -> [ 1 2 **4 5** 8 ]
51
51
52
52
[ 1 2 4 **5 8**] -> [ 1 2 4 **5 8**]
53
-
54
-
This is the same for the forth and fifth passes.
53
+
`
54
+
This is the same for the fourth and fifth passes.
55
55
56
56
#### Code
57
57
```swift
@@ -68,7 +68,7 @@ return array
68
68
```
69
69
70
70
#### Optimization
71
-
The bubble sort algorithm can be easily optimized by observing that the `n-th` pass finds the `n-th` largest element and puts it into its final place. So, the inner loop can avoid looking at the last `n-1` items when running for the `n-th` time:
71
+
Notice that the `n-th` pass finds the `n-th` largest element and puts it into its final place. With this observation, the bubble sort algorithm can be optimized by stopping the inner loop from looking at the last `n-1` items when running for the `n-th` time:
72
72
73
73
```swift
74
74
for i in0..<array.count {
@@ -83,7 +83,7 @@ for i in 0..<array.count {
83
83
return array
84
84
```
85
85
86
-
The only change made was on the second line, changing the interval from `1..<array.count` to `1..<array.count - i`, effectively cutting the number of comparisons by half.
86
+
The only change made was on the second line by adjusting the interval from `1..<array.count` to `1..<array.count - i`, effectively cutting the number of comparisons in half.
87
87
88
88
The ordering with the optimized code would look something like this for the array `[5, 1, 4, 2, 8]`:
89
89
@@ -113,11 +113,11 @@ The ordering with the optimized code would look something like this for the arra
113
113
##### Fourth Pass
114
114
[**1 2** 4 5 8 ] -> [**1 2** 4 5 8 ]
115
115
116
-
There is no Fifth pass
116
+
There is no fifth pass
117
117
118
118
#### Conclusion
119
119
120
-
Even with the proposed optimizations, this is still a terribly inefficient sorting algorithm. A good alternative is [Merge Sort](https://github.com/raywenderlich/swift-algorithm-club/tree/master/Merge%20Sort), that not only is better performing, has a similar degree of dificulty to implement.
120
+
Even with the proposed optimizations, bubble sort remains a terribly inefficient sorting algorithm. A good alternative is [Merge Sort](https://github.com/raywenderlich/swift-algorithm-club/tree/master/Merge%20Sort), which not only performs better, but also is equally as easy to implement.
121
121
122
122
*Updated for the Swift Algorithm Club by Julio Brazil*
0 commit comments